前回

grg.hatenablog.com

はじめに

前回はニューラルネットをtorchパッケージを使用して実装してみました。今回は変分オートエンコーダー（VAE）を同じような形で実装していきます。 VAEは今後紹介する生成モデルの基礎となるモデルになります。今までもそうでしたが、参考書のpythonコードをすべてRコードで再現するのではなく、それらを要約しつつ個人的にわかりやすいように一部変更しながらコードを書いています。 その点について留意いただきながらご覧になっていただけますと幸いです。

STEP 7.1：混合ガウスモデル（GMM）と変分オートエンコーダー（VAE）の違いについて

振り返りも含めてGMMとVAEの違いについて触れていきます。GMMは正規分布を複数（K個）用意して、その中の正規分布を1つ選んでそこからデータが得られたと考える生成モデルです。つまり、潜在変数はK個のうち1つを選択するカテゴリカル分布に従います。 一方、VAEは潜在変数を正規分布として設定し、その潜在変数をニューラルネットに通すことでデータを再現するモデルです。

記載した通り、GMMとVAEは潜在変数の設定が異なります。GMMはカテゴリカル分布なので離散的な分布ですが、VAEは正規分布なので連続的な分布です。そのため、より細かい粒度で潜在変数を表現することができる可能性があります。 また、GMMは潜在変数から選択した正規分布からデータを得られたと仮定しますが、VAEはニューラルネットを用いているためより柔軟な表現力を持つと考えられます。

一方、VAEはGMMより複雑なモデルであるため、パラメータ推定は一般的により困難になります。そのため、例えばデータ数が少ないと収束しなかったり局所解に陥る可能性が相対的に高いと考えられ、そのようなモデルリスクがあることには留意が必要かもしれません。

STEP 7.2：VAEの学習

GMMとVAEの違いについて簡単に紹介しましたが、大きな違いとしては潜在変数が離散から連続に変わったことです。その違いにより前回紹介したEMアルゴリズムを直接使用することができず、学習するためにはひと手間かかってしまいます。 その点について触れていきます。まず、VAEの対数尤度は以下のように計算できます。

EMアルゴリズムと同様に第一項目がELBO、第二項目がKLダイバージェンスになります。EMアルゴリズムではとすればよかったのですが、VAEでは直接を求めることが難しいのでこの手が使えません。 そのため、と仮定して計算していきます。このように直接計算不可能な分布に対して、その分布を近似する計算可能な分布を設定して計算していく方法を変分近似や変分ベイズと呼ばれます。変分オートエンコーダーの変分はここから来ています。

では、このをどのように推定していけばよいのでしょうか？結論から言うと、ELBOにもが含まれているのでELBOが最大になるようにを更新すれば、それが結局がに一番近づくようになります。これは、そもそもの対数尤度はをパラメータとして持たないので、をどのように動かしても対数尤度の値は変わりません。つまり、第一項目のELBOがに対して最大化される→第二項目のKLダイバージェンスが最小になる→がに一番近づくということになります。

では、より具体的にの推定の仕方を見ていきます。は潜在変数の分布を決定付けるパラメータなので、データが得られたときに潜在変数がどのような分布になるかがわかればOKです。 よって、VAEではデータをインプットして潜在変数の分布のパラメータであるを出力するニューラルネットを用いて推定していきます。このようにデータから潜在変数のパラメータを求めるのは、エンコーダー（Encoder）と呼ばれています。 逆に潜在変数からデータを生成するモデルをデコーダー（Decoder）と呼びます。（※以降、デコーダー・エンコーダーの意味合いは知っている前提で文章やコードを記載していきますのでご注意ください）

ここまでの内容をまとめますと、まずエンコーダーでデータから潜在変数の分布を推定します。そして、その分布から得られた潜在変数をデコーダーに通してデータを生成します。 このようにデータをインプットして、そのデータを複製するようなモデルのことをオートエンコーダーと言い、先ほどの変分の話と合わせて変分オートエンコーダー（VAE）と呼ばれています。 VAEのパラメータを決定できれば、後は潜在変数を好きなだけ生成してデコーダーに通せば、もともとのデータの特徴を持ったデータを生成することができるようになります。

STEP 7.2：VAEの実装

ここではVAEの実装をしていきます。詳細な計算は参考書をご覧になっていただければと思いますが、ELBOは以下のように近似計算することができます。 ここではモデルからサンプリングしたデータになります。これはELBO内の期待値の計算をするためにデータを1つサンプリングした結果を基にその期待値を計算しています。 もし、期待値計算するときにもっとデータを増やした方がよいということであれば、複数データをサンプリングしてその結果を平均すればOKです。 参考書によると、データ数が1個でもVAEの場合はうまく推定ができる可能性が高いとのことです。

このELBOを用いて実装したRコードは以下の通りです。

#Encoderを実装
Encoder <-nn_module(
  initialize =function(input_dim, hidden_dim, latent_dim){
    self$linear =nn_linear(input_dim, hidden_dim)
    self$linear_mu =nn_linear(hidden_dim, latent_dim)
    self$linear_logvar =nn_linear(hidden_dim, latent_dim)},
  forward =function(x){
    h = self$linear(x)
    h =nnf_relu(h)
    mu = self$linear_mu(h)
    logvar = self$linear_logvar(h)
    sigma =torch_exp(0.5* logvar)
    latent_params =list(mu, sigma)return(latent_params)})#Decoderを実装
Decoder <-nn_module(
  initialize =function(latent_dim, hidden_dim, output_dim){
    self$linear_1 =nn_linear(latent_dim, hidden_dim)
    self$linear_2 =nn_linear(hidden_dim, output_dim)},
  forward =function(z){
    h = self$linear_1(z)
    h =nnf_relu(h)
    h = self$linear_2(h)
    x_hat =nnf_sigmoid(h)return(x_hat)})#パラメータ推定のためのreparameterize
reparameterize =function(params){
  mus = params[[1]]
  sigmas = params[[2]]
  
  eps =torch_randn_like(sigmas)
  z = mus + eps * sigmas
  
  return(z)}#VAEを実装
VAE <-nn_module(
  initialize =function(input_dim, hidden_dim, latent_dim){
    self$encoder =Encoder(input_dim,hidden_dim,latent_dim)
    self$decoder =Decoder(latent_dim,hidden_dim,input_dim)},
  getloss =function(x){
    params = self$encoder(x)
    z =reparameterize(params)
    x_hat = self$decoder(z)
    
    L1 =nnf_mse_loss(x_hat,x, reduction ="sum")
    L2 =-torch_sum(1+torch_log(params[[2]]**2)- params[[1]]**2- params[[2]]**2)return((L1+L2)/batch_size)})

エンコーダーを実装する際、list型でを返すような関数を組んでいます。 pythonの場合は複数の返値を並行して設定することができますが、Rの場合はこのようにlist型で返すことが一般的な気がします。 ここら辺はpythonのほうが実装しやすいかもしれないですね。

STEP 7.2：VAEの学習

最後に実際のデータをVAEに通して学習してみましょう。 先程のVAEコードにMNISTデータをインプットして学習していきます。MNISTデータはtorchvisionパッケージから取得しています。 先程のRコードもそうですが、ここら辺になってくると参考書のpythonコードとRコードでは記法が若干異なってきますね。

library(torchvision)# ハイパーパラメータの設定
input_dim =784
hidden_dim =200
latent_dim =20
epochs =1000
learning_rate =3*10^-4
batch_size =32

ds <-mnist_dataset(
  root ="./data",
  train =TRUE,# default
  download =TRUE,
  transform =function(x){
    y = x %>%transform_to_tensor()
    y =torch_flatten(y)})

dl <-dataloader(ds, batch_size = batch_size, shuffle =TRUE)

model =VAE(input_dim, hidden_dim, latent_dim)
optimizer =optim_adam(model$parameters, lr = learning_rate)
losses =c()

x = dl %>%dataloader_make_iter()%>%dataloader_next()for(epoch in1:epochs){
  loss_sum =0
  cnt =0for(in_x in1:batch_size){
    optimizer$zero_grad()
    loss = model$getloss(x$x[in_x])
    loss$backward()
    optimizer$step()
    
    loss_sum = loss_sum + loss$item()
    cnt = cnt +1}
  
  loss_avg = loss_sum / cnt
  losses =c(losses, loss_avg)print(loss_avg)}

losses_plot =bind_cols(1:epochs,losses)names(losses_plot)=c("epochs","losses")ggplot(losses_plot)+geom_line(aes(x=epochs, y=losses))

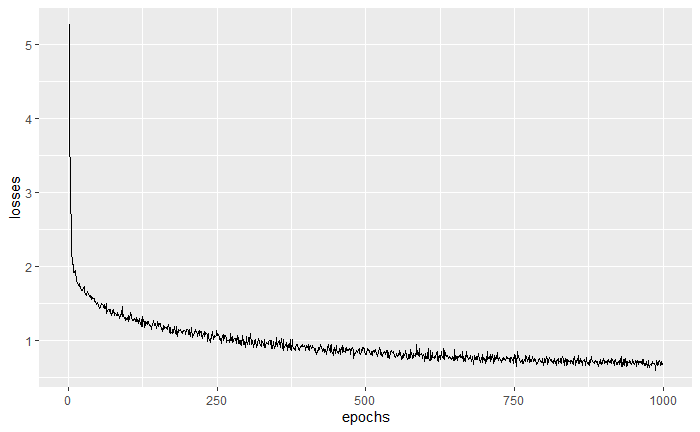
参考書に載っているVAEの損失関数とは水準感と推移の仕方が異なっているように見えますが、損失自体は問題なく小さくなっています。（参考書のグラフは滑らか過ぎるので何か加工している？） また、十分に学習するためにはエポック数を大きくする必要があった点も参考書とは異なっていました。あくまで参考書ということで、本稿では自分である程度満足する結果が出るように設定を変えたりしていますのでご注意ください。 最後に、学習したVAEで画像を生成してみようかと思います。

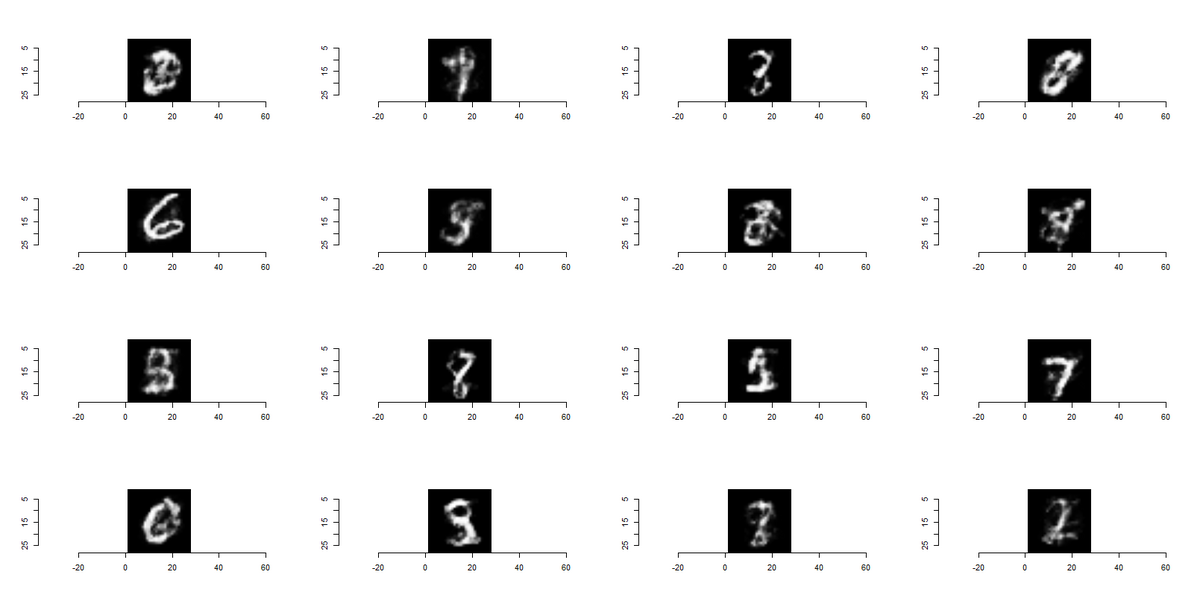
library(imager)

plot_list =list()for(i in1:16){with_no_grad({
    sample_size =1
    z =torch_randn(sample_size, latent_dim)
    x = model$decoder(z)
    generated_images = x$view(c(sample_size,28,28))})
  
  tmp = generated_images %>%as.array()
  tmp_min =min(tmp)
  tmp_max =max(tmp)
  tmp =(tmp - tmp_min)/ tmp_max
  plot_list[[i]]=as.cimg(t(tmp[1,,]))}par(mfrow =c(4,4))for(i in1:16){plot(plot_list[[i]])}

ここら辺の画像の出し方はpythonのほうが楽な気がします（私がRにおける画像の扱いに慣れていないことが大きいのですが・・・）。 画像の出し方は乱数を発生させてVAEのデコーダーにインプットすれば作成することができます。 少し画質が荒い感じもしますが、「８」だったり「６」だったり様々な数値の画像が得られていることがわかります。 ここからVAEの学習は一定程度うまくいっているように思えます。

まとめ

今回はVAEを実装してみました。徐々にRコードとpythonコードに差が出始めてきたので、参考書を見るだけでは実装が難しくなってきました・・・。 少しずつ記事を書くスピードが落ちるかもしれませんが、次回以降の章も頑張って実装していこうかと思います。